https://www.acmicpc.net/problem/14889

1.문제설명

N명이 있을 때 N/2로 각각 팀을 나눠주고

문제에서 주어진 점수표로 각각 팀의 점수를 계산해

차이가 최소가 되도록 구해주어야한다.

2.접근방법[알고리즘]

2-1. 팀 나누기

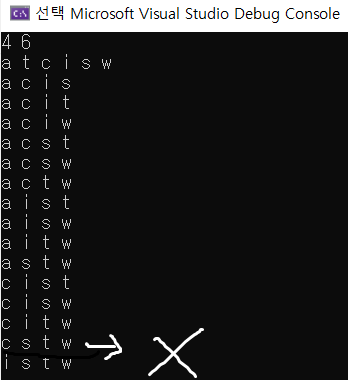
DFS를 돌면서 조합으로 n명중 n/2명을 뽑아준다.

bool 타입 배열 ch에 뽑힌 번호는 true 안 뽑힌 번호는 false로 지정해줘서 두 팀으로 나눠줄 수 있다.

두 팀으로 나눠준 후 점수를 구해준다.

void DFS(int cur, int L) {
	if (L == n / 2) {
		ans = min(ans, cal());
	}
	else {
		for (int i = cur+1; i <= n; i++) {
			ch[i] = true;
			DFS(i, L + 1);
			ch[i] = false;
		}
	}
}

2-2. 점수구하기

int cal() {
	int point1=0, point2=0;
	for (int i = 1; i <= n; i++){
		for (int j = 1; j <= n; j++){
			if (ch[i] == true && ch[j] == true) 
				point1 += arr[i][j];
			if (ch[i] == false && ch[j] == false) 
				point2 += arr[i][j];
		}
	}
	return abs(point1 - point2);
}

만약 1과 2가 한팀이라고 가정하면

그 팀의 점수는 arr[1][2] + arr[2][1]이다.

만약 1, 2, 3이 한팀이라면

arr[1][2] + arr[1][3] + arr[2][1] + arr[2][3] + arr[3][1] + arr[3][2]

이렇게 된다.

참고로 문제에서 arr[i][i] = 0 으로 주기 때문에

arr[1][2] + arr[1][3] + arr[2][1] + arr[2][3] + arr[3][1] + arr[3][2]는

arr[1][1] + arr[1][2] + arr[1][3] + arr[2][1] + arr[2][2] + arr[2][3] + arr[3][1] + arr[3][2] + arr[3][3]과 동일하다.

그래서 위 코드처럼 하면 각 팀의 점수를 구해줄 수 있다.

점수를 구하는 과정도 DFS로 순열을 구현해서 할 수 있겠으나 

귀찮기도하고 이문제에서는 원소가 두개로 지정되어있으므로 for문으로 구현하는게 편하다.

3. 문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int arr[22][22], n, ans=INT_MAX;
bool ch[22];

//팀별 점수 계산해주는 함수 
int cal() {
	int point1=0, point2=0;
	for (int i = 1; i <= n; i++){
		for (int j = 1; j <= n; j++){
			if (ch[i] == true && ch[j] == true) 
				point1 += arr[i][j];
			if (ch[i] == false && ch[j] == false) 
				point2 += arr[i][j];
		}
	}
	return abs(point1 - point2);
}


//조합으로 팀 나눠주는 함수 
void DFS(int cur, int L) {
	if (L == n / 2) {
		ans = min(ans, cal());
	}
	else {
		for (int i = cur+1; i <= n; i++) {
			ch[i] = true;
			DFS(i, L + 1);
			ch[i] = false;
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> arr[i][j];
		}
	}

	DFS(0, 0);

	cout << ans;
}

https://www.acmicpc.net/problem/2580

문제풀이코드는 맨 하단에 있습니다.

1.문제설명

스도쿠를 푸는 문제이다.

비어있는 칸을 채워주면 된다.

규칙은 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다

굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.

문제입력

0 3 5 4 6 9 2 7 8
7 8 2 1 0 5 6 0 9
0 6 0 2 7 8 1 3 5
3 2 1 0 4 6 8 9 7
8 0 4 9 1 3 5 0 6
5 9 6 8 2 0 4 1 3
9 1 7 6 5 2 0 8 0
6 0 3 7 0 1 9 5 2
2 5 8 3 9 4 7 6 0

빈칸은 0으로 입력된다.

출력은 스도쿠로 가능한 방법 중 하나를 출력하면 된다.

2.접근방법[알고리즘]

비워있는 칸을 규칙에 따라서 채워야한다.

빈칸, 즉 스도쿠에서 입력값이 0인 좌표를 배열에 저장한다.

일단 빈칸에 들어갈 숫자는 1~9 중 하나이고

가로줄,세로줄, 3x3 정사각형 안에 이미 등장했는지 안했는지 체크해준다.

2-1 체크 함수

//value 사용 할 수 있는지 체크하는 함수
//리턴 값 true면 사용가능
bool check(int x, int y, int value) {
	//가로 세로에서 value 이미 존재하는지 탐색
	for (int i = 0; i < 9; i++) {
		if(arr[i][y] == value) return false;
		if (arr[x][i] == value) return false;
	}
	//3x3 칸 내에 value 이미 존재하는지 탐색
	int part_x = x / 3;
	int part_y = y / 3;
	part_x *= 3;
	part_y *= 3;
	for (int i = part_x; i < part_x + 3; i++) {
		for (int j = part_y; j < part_y + 3; j++) {
			if (arr[i][j] == value) return false;
		}
	}
	return true;
}

check함수를 이용해 이미 등장한 숫자가 아니라면 숫자를 넣어보고

다음 빈칸을 똑같은 과정을 수행해본다.

그리고 모든 빈칸에 숫자를 넣는다면 함수를 종료해준다.

그리고 정답이 나올 때까지 모든 경우에 탐색을 해봐야하므로

빈칸에 숫자를 넣고 DFS를 시행해보고 다시 그 빈칸을 초기화해주어야한다.

초기화해주지 않으면 모든 숫자가 0 인 경우에 대해서 스도쿠를 꽉 채우지 못한다.

DFS함수

void DFS(int cur) {
	if (isend == true) return;
	if (cur == L) {
		for (int i = 0; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				cout << arr[i][j] << ' ';
			}
			cout << '\n';
		}
		isend = true;
	}
	else{
		int nx = v[cur].first;
		int ny = v[cur].second;
		for (int i = 1; i <= 9; i++) {
			if (check(nx, ny, i)) {
				arr[nx][ny] = i;
				DFS(cur + 1);
				//위에 DFS가 정답이 아닐 수도 있으니 초기화하고 돌아줘야한다.
				arr[nx][ny] = 0;
			}
		}
	}
}

스도쿠 반례

0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int arr[9][9], L;
vector<pair<int, int> > v;

bool isend = false;
//value 사용 할 수 있는지 체크하는 함수
//리턴 값 true면 사용가능
bool check(int x, int y, int value) {
	for (int i = 0; i < 9; i++) {
		if(arr[i][y] == value) return false;
		if (arr[x][i] == value) return false;
	}
	//3x3 칸 내에 value 이미 존재하는지 탐색
	int part_x = x / 3;
	int part_y = y / 3;
	part_x *= 3;
	part_y *= 3;
	for (int i = part_x; i < part_x + 3; i++) {
		for (int j = part_y; j < part_y + 3; j++) {
			if (arr[i][j] == value) return false;
		}
	}
	return true;
}

void DFS(int cur) {
	if (isend == true) return;
	if (cur == L) {
		for (int i = 0; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				cout << arr[i][j] << ' ';
			}
			cout << '\n';
		}
		isend = true;
	}
	else{
		int nx = v[cur].first;
		int ny = v[cur].second;
		for (int i = 1; i <= 9; i++) {
			if (check(nx, ny, i)) {
				arr[nx][ny] = i;
				DFS(cur + 1);
				//위에 DFS가 정답이 아닐 수도 있으니 초기화하고 돌아줘야한다.
				arr[nx][ny] = 0;
			}
		}
	}
}


int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	for (int i = 0; i < 9; i++) {
		for (int j = 0; j < 9; j++) {
			cin >> arr[i][j];
			if (arr[i][j] == 0) {
				v.push_back({ i,j });
			}
		}
	}
	L = v.size();
	DFS(0);
}

4. 문제풀이후기

빈칸에 넣을 수 있는 숫자를 계속 넣어보면서

백트래킹을 수행하면 풀 수 있는 문제였습니다.

https://www.acmicpc.net/problem/1987

1.문제설명

2 4
CAAB
ADCB

다음과 같이 알파벳으로 이루어진 보드가 주어질 때

각 알파벳은 한 번씩만 방문할 수 있다.

좌측 상단(C)에서 시작해서 상하좌우로 이동하여

이동할 수 있는 최대 칸 수를 구해야한다.

D로 이동하면 D에서 상하좌우를 보면

위는 이미 방문해서 갈 수 없고 좌우는 이미 지난 알파벳이어서 방문할 수 없어서

D에서 깊이탐색이 끝나게 되고,

이동 거리는 3이다.

2.접근방법[알고리즘]

이 문제는 말이 최대한 몇칸을 움직일 수 있는지 구해야하는 문제다.

보통 DFS나 BFS로 최단거리를 많이 구하는데 이 문제는 다르게

이동할 수 있는 최대 거리를 구해야한다.

그리고 각 알파벳 마다 한번 씩만 방문할 수 있다.

방문한 알파벳을 저장해주면서 DFS 탐색을 돌아

최대 이동 거리를 갱신해주어야 한다.

2-1. 방문한 노드 좌표는 따로 저장을 안해주어도 되나?

방문한 알파벳을 저장해주면 알파벳 정보에

방문한 노드 정보까지 자연스럽게 포함된다

예를 들어 전에 방문한 노드가 C라면 C를 저장해주면

노드 번호를 따로 저장해주지 않아도 다음 노드가 C이면 탐색을 하지 않는다.

그러므로 방문한 알파벳만 저장하고 체크하면 된다.

2-2. DFS 코드

DFS(x좌표, y좌표, 이동거리) 이렇게 매개변수를 두고

dist가 최대일 때마다 갱신해주면서 깊이탐색 했다.

bool 배열 ch_alpha에 해당 알파벳이 이미 방문된 알파벳인지 체크해준다.

백트래킹을 돌면서 최대 이동거리를 갱신한다.

int r, c, ans;
char arr[21][21];
bool ch_alpha[26];

int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };

void DFS(int x, int y, int dist) {
	
	ans = max(ans, dist);

	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (nx < 0 || nx >= r || ny < 0 || ny >= c) continue;
		
		int next_alpha = arr[nx][ny] - 'A';
		if (ch_alpha[next_alpha] == 0) {
			ch_alpha[next_alpha] = 1;
			DFS(nx, ny, dist + 1);
			ch_alpha[next_alpha] = 0;
		}
	}
}

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int r, c, ans;
char arr[21][21];
bool ch_alpha[26];

int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };

void DFS(int x, int y, int dist) {
	
	ans = max(ans, dist);

	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (nx < 0 || nx >= r || ny < 0 || ny >= c) continue;
		
		int next_alpha = arr[nx][ny] - 'A';
		if (ch_alpha[next_alpha] == 0) {
			ch_alpha[next_alpha] = 1;
			DFS(nx, ny, dist + 1);
			ch_alpha[next_alpha] = 0;
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> r >> c;

	for (int i = 0; i < r; i++) {
		for (int j = 0; j < c; j++) {
			cin >> arr[i][j];
		}
	}

	ch_alpha[arr[0][0] - 'A'] = 1;
	DFS(0, 0, 1);

	cout << ans << '\n';

}

https://www.acmicpc.net/problem/1759

1. 문제설명

순열이나 조합을 만드는 문제와 비슷하다. 차이점은 숫자 대신 문자를 출력한다는 점이다.

조건에서 구해야 하는 암호는 항상 사전순으로 이루어져있어야하고

최소 한 개의 모음(a, e, i, o, u)과 최소 두 개의 자음으로 구성되어 있어야한다.

입력

4 6
a t c i s w

출력

acis
acit
aciw
acst
acsw
actw
aist
aisw
aitw
astw
cist
cisw
citw
istw

2. 접근 방법[알고리즘]

먼저 증가하는 순열(조합)을 만들고 그 순열에 알파벳 순으로 덮어준다고 생각하면 쉽다.

다만 문제에서 사전순이라는 조건과 모음과 자음의 갯수 조건이 있으므로

우선 알파벳 순열을 만들어주고 그 알파벳 순열이 조건에 부합한다면 출력해주면 된다.

우선 증가하는 순열을 만들어보자. 

6개의 숫자에서 4개의 숫자를 뽑는 조합을 만든다고 생각해도 동일하다.

#include <bits/stdc++.h>
using namespace std;

int L, C, path[20], ch[20] , t=1;
char a[20], ans[20];

void DFS(int cur) {
	if (t == L+1) {
		for (int i = 1; i <= L; i++) {
			cout << path[i] << ' ';
		}
		cout << '\n';

	}
	else {
		for (int i = cur; i <= C; i++) {
			if (ch[i] == 0) {
				ch[i] = 1;
				path[t++] = i;
				DFS(i);
				ch[i] = 0;
				t--;
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> L >> C;


	DFS(1);
}

이제 각 숫자에 해당 알파벳을 적용하면 된다

알파벳은 문제 조건에 따라 사전순으로 정렬되어야한다.

a t c i s w

이제 알파벳 까지 적용해서 잘 만들었다.

하지만 cstw는 문제 조건에서 모음이 한개이상 있어야하므로 출력되면 안된다.

↓ 지금 단계 까지의 코드

#include <bits/stdc++.h>
using namespace std;

int L, C, path[20], ch[20] , t=1;
char a[20], ans[20];

void DFS(int cur) {
	if (t == L+1) {
		int cnt1 = 0;
		//for (int i = 1; i <= L; i++) {
		//	ans[i] = a[path[i]];
		//	if (ans[i] == 'a' || ans[i] == 'e' ||
		//		ans[i] == 'i' || ans[i] == 'o' || ans[i] == 'u') {
		//		cnt1++;
		//	}
		//}

		//if (cnt1 >= 1 && L - cnt1 >= 2) {
		//	for (int i = 1; i <= L; i++) {
		//		cout << ans[i];
		//	}
		//	cout << '\n';

		//}

		for (int i = 1; i <= L; i++) {
			cout << a[path[i]] << ' ';
		}
		cout << '\n';

	}
	else {
		for (int i = cur; i <= C; i++) {
			if (ch[i] == 0) {
				ch[i] = 1;
				path[t++] = i;
				DFS(i);
				ch[i] = 0;
				t--;
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> L >> C;

	for (int i = 1; i <=C; i++) {
		cin >> a[i];
	}
	sort(a+1 , a + 1 + C);

	DFS(1);
}

마지막으로 출력하기전에 모음과 자음 갯수를 카운트해

조건에 부합하면 출력하면된다.

cnt1 변수로 모음갯수만 세서 전체 알파벳 갯수인 L에서 cnt1을 빼주면 자음갯수를 구할 수 있다.

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int L, C, path[20], ch[20] , t=1;
char a[20], ans[20];

void DFS(int cur) {
	if (t == L+1) {
		int cnt1 = 0;
		for (int i = 1; i <= L; i++) {
			ans[i] = a[path[i]];
			if (ans[i] == 'a' || ans[i] == 'e' ||
				ans[i] == 'i' || ans[i] == 'o' || ans[i] == 'u') {
				cnt1++;
			}
		}

		if (cnt1 >= 1 && L - cnt1 >= 2) {
			for (int i = 1; i <= L; i++) {
				cout << ans[i];
			}
			cout << '\n';

		}
	}
	else {
		for (int i = cur; i <= C; i++) {
			if (ch[i] == 0) {
				ch[i] = 1;
				path[t++] = i;
				DFS(i);
				ch[i] = 0;
				t--;
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> L >> C;

	for (int i = 1; i <=C; i++) {
		cin >> a[i];
	}
	sort(a+1 , a + 1 + C);

	DFS(1);
}

DFS, 백트래킹을 이용하여 조합을 만들어주고

문제 조건을 적용하면 해결되는 문제이다.

https://www.acmicpc.net/problem/2583

1. 문제설명

모눈 종이에 직사각형이 그려져 있을 때

직사각형이 색칠되어 있지 않은 남은 부분들의 갯수와 부분들의 넓이를 구해서

오름차순으로 정렬해 출력하면 된다.

사각형의 갯수가 곧 넓이가 된다.

2. 접근방법[알고리즘]

색칠된 부분을 저장하기 위해 M*N 배열을 만들어야한다.

좌표를 설정하는 걸 조심해야한다.

N, M은 7,5지만 이건 꼭짓점이고 실제로

해당 칸 마다 좌표를 부여하면 (0,0) ~ (6,4)까지만 사용 한다.

입력

5 7 3
0 2 4 4
1 1 2 5
4 0 6 2

arr[i][j]의 값에 색칠되었다면 -1을 저장하고 색칠되지 않았다면 0을 저장해준다.

색칠해줄 때도 (0,2)에서 (4,4)까지 칠해주는게 아니라 (0,2)에서 (3,3)까지 칠해주어야한다.

이유는 위와 동일하게 (4,4)는 사각형의 해당 좌표가아니라 꼭짓점이기 때문이다.

	//직사각형 -1로 칠하기
	for (int i = 0; i < k; i++) {
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		for (int j = y1; j < y2; j++) { // y1 ~ <y2 까지 돌아야 한다
			for (int k = x1; k < x2; k++) { // x1 ~ <x2 까지 돌아야 한다
				arr[j][k] = -1;
			}
		}
	}

그리고 arr배열 값이 -1인 좌표는 BFS를 돌지 않고

arr배열이 0인 값만 탐색한다.

이제 arr배열을 돌면서 값이 0인 좌표를 발견하면

BFS를 실행하면서 arr 값에 사각형의 개수를 저장해준다.

BFS 실행 코드

arr값이 0인 좌표를 발견할 때 arr 값을 1로 저장해준다. 

cnt 변수는 arr값이 0인 좌표를 발견했을 때 +1 해주어 전체 하얀 부분의 개수를 구할 수 있다.

this_area 변수는 BFS를 돌면서 0인좌표를 발견할 때마다 +1 해주어 해당 부분의 넓이를 저장해준다

그리고 Q가 empty가 되어 BFS가 끝나면 해당 하얀 부분을 다 탐색했다는 뜻이므로

this_area 변수의 값을 ans에 저장해준다.

이렇게 모든 좌표에대해 탐색하면 하얀 부분의 넓이를 모두 구할 수 있다.

	queue<pair<int, int> > Q;

	for (int i = 0; i < m; i++) {
		for (int j = 0; j < n; j++) {
			if (arr[i][j] == 0) {
				cnt++;
				arr[i][j] = 1;
				int this_area = 1;
				Q.push(make_pair(i, j));

				while (!Q.empty()) {
					int cur_x = Q.front().first;
					int cur_y = Q.front().second;
					Q.pop();

					for (int k = 0; k < 4; k++) {
						int nx = cur_x + dx[k];
						int ny = cur_y + dy[k];
						if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
						if (arr[nx][ny] == 0) {
							arr[nx][ny] = ++this_area;
							Q.push({ nx,ny });
						}
					}
				}
				ans.push_back(this_area);
			}
		}
	}

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };
int n,m,k, cnt, arr[101][101];
vector<int> ans;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	//색칠영역 -1로 두고
	//-1이 아닌 곳 BFS 돌면서 넓이 구해주면 된다
	cin >> m >> n >> k;

	//직사각형 -1로 칠하기
	for (int i = 0; i < k; i++) {
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		for (int j = y1; j < y2; j++) {
			for (int k = x1; k < x2; k++) {
				arr[j][k] = -1;
			}
		}
	}

	//직사각형 확인
	//cout << "------------------------\n";
	//for (int i = 0; i < m; i++) {
	//	for (int j = 0; j < n; j++) {
	//		cout << arr[i][j] << ' ';
	//	}
	//	cout << '\n';
	//}
	//cout << "-------------------\n";

	queue<pair<int, int> > Q;

	for (int i = 0; i < m; i++) {
		for (int j = 0; j < n; j++) {
			if (arr[i][j] == 0) {
				cnt++;
				arr[i][j] = 1;
				int this_area = 1;
				Q.push(make_pair(i, j));

				while (!Q.empty()) {
					int cur_x = Q.front().first;
					int cur_y = Q.front().second;
					Q.pop();

					for (int k = 0; k < 4; k++) {
						int nx = cur_x + dx[k];
						int ny = cur_y + dy[k];
						if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
						if (arr[nx][ny] == 0) {
							arr[nx][ny] = ++this_area;
							Q.push({ nx,ny });
						}
					}
				}
				ans.push_back(this_area);
			}
		}
	}


	//결과 확인
	//for (int i = 0; i < m; i++) {
	//	for (int j = 0; j < n; j++) {
	//		cout << arr[i][j] << ' ';
	//	}
	//	cout << '\n';
	//}
	//cout << "-------------------\n";


	//정답 출력
	cout << cnt << '\n';
	sort(ans.begin(), ans.end());
	for (int i = 0; i < ans.size(); i++) {
		cout << ans[i] << ' ';
	}

}

일반적인 BFS탐색 문제와 비슷하다.

다만 좌표설정하는 부분을 잘 유의해야할 필요가 있다.

https://www.acmicpc.net/problem/16964

1. 문제설명

입력으로 N개의 노드가 주어지고 노드간의 연결관계가 주어진다.

그리고 마지막 입력으로 DFS 방문 순서가 주어진다.

노드간의 연결관계를 바탕으로 깊이우선탐색을 할 때

주어진 방문 순서처럼 방문할 수 있는지 여부를 묻는 문제이다.

2.접근방법[알고리즘]

접근 방법은 문제 이름부터 DFS이기 때문에 쉽게 알 수 있다.

하지만 이 문제를 푸는 게 생각보다 많이 어려웠다.

그동안 DFS를 이용해 최단 거리나 백트래킹 위주 문제를 많이 풀다보니

처음 이 문제를 봤을 때

"주어진 정점과 간선을 통해 DFS로 탐색할 수 있는 모든 방문순서를 구해야하나?" 생각했다

그렇게 할 수도 있겠지만 그러면 시간초과할 것 같았다.

이 문제는 DFS의 방문 순서에대해 생각해보아야 해결 할 수 있다.

예제 입력을 갖고 생각해보자.

4
1 2
1 3
2 4
1 2 3 4

이렇게 주어졌을 때 그래프는 다음과 같다

DFS로 탐색 할 때 1번 노드에서 출발하면

2번, 3번 중 방문 순서를 택해야 한다.

2번을 먼저 방문하기로 택하면 

1 2 4 3 이렇게 탐색 하고

3번을 먼저 택하면 1 3 2 4 순서로 탐색하게 된다.

2번 노드와 3번 노드중 어떤 걸 먼저 탐색하게 해야 할까?

보통 일반적인 DFS나 BFS 문제에서는 어떤 노드를 먼저 탐색하게끔 문제를 만들지 않는다.

결과적으로 다 탐색한 뒤 어떤 결괏값을 갖는지를 많이 물어본다.

하지만 이 문제에서는 어떤 노드를 먼저 탐색할지 정해주는 과정이 필수적이다.

문제 입력 마지막 줄에 예상 DFS 탐색 순서를 준다.

만약 위처럼 1 2 3 4 이렇게 주어졌다면

우리는 깊이 우선 탐색을 할 때 2번 노드를 3번노드 보다 먼저 택해야한다.

만약 주어진 예상 DFS 탐색 순서가 1 3 2 4 라면

우리는 깊이 우선 탐색을 할 때 3번 노드를 2번노드 보다 먼저 택해야한다.

즉 마지막 예상 DFS 탐색 순서를 바탕으로해서

어떤 노드를 먼저 탐색해야할지 정해주고,

정해진 노드 탐색 순서를 바탕으로 DFS를 수행했을 때

예상 DFS 탐색 순서와 일치하는지 확인하는 문제이다.

노드간의 연결 관계를 인접리스트로 만들고,

인접리스트의 노드 순서를 정해진 노드 탐색 순서로 정렬한 뒤

깊이우선탐색을 실행해야 한다.

이해를 돕기 위해 다른 입력으로 생각해보자

(마지막 줄, DFS예상 탐색 순서만 다르다)

4
1 2
1 3
2 4
1 3 2 4

order

1,2,3,4 노드가 있을 때

항상 탐색 순서는

1번 노드가 첫번째

3번 노드가 두번째

2번 노드가 세번째

4번 노드가 네번째로 돌아야한다.

이를 위해 order 배열에 순서에 해당하는 노드를 저장해준다

order[2] = 3이면 우선 순위 두번째 노드가 3이라는 뜻이다.

그리고 이런 우선순위를 바탕으로 인접리스트의 노드들을 정렬해준다.

각 노드의 탐색 우선순위를 지정해주기 위한 코드다.

bool comp(int a, int b){
	return order[a] < order[b];
}
    
for(int i=1; i<=n; i++){
	int node;
	cin >> node; 
	given_path[i] = node;
	order[node] = i;
}
	
for(int i=1; i<=n; i++){
	sort(ad[i].begin(), ad[i].end(), comp);
}

sort를 시행하기 전

1번 노드는 2번 노드를 먼저 탐색한다.

sort 한 후 3번이 2번보다 우선순위가 높기 때문에 2 앞으로 온다.

이제 DFS를 돌면 2보다 먼저 탐색된다.

다시 설명하자면,

이렇게 해주는 이유는

문제 입력에서 1,3,2,4 순으로 탐색을 할 수 있는지 물어보았기 때문에 3은 무조건 2보다 먼저 탐색되야한다.

문제입력에 주어진 조건을 바탕으로 

각 노드마다 우선순위를 적용해준 뒤 탐색한 후 1,3,2,4 순으로 탐색이 되는지 확인하기 위함이다.

3. 문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

vector<int> ad[100001]; 
int order[100001], given_path[100001], DFS_path[100001], L=1;
bool ch[100001];

bool comp(int a, int b){
	return order[a] < order[b];
}

void DFS(int x){
	ch[x] = 1;
	DFS_path[L++] = x;
	
	for(int i=0; i<ad[x].size();i++){
		int nx = ad[x][i];
		if(ch[nx]==0) DFS(nx);
	}
}


int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n;
	cin >> n;
	
	for(int i=1; i<n; i++){
		int node1, node2;
		cin >> node1 >> node2;
		ad[node1].push_back(node2);
		ad[node2].push_back(node1);
	}
	
	// 각 노드마다 순서를 정해준다  
	for(int i=1; i<=n; i++){
		int node;
		cin >> node; 
		given_path[i] = node;
		order[node] = i;
	}
	
	for(int i=1; i<=n; i++){
		sort(ad[i].begin(), ad[i].end(), comp);
	}
	
	//1번부터 돌기 떄문  
	DFS(1);
	for(int i=1; i<=n; i++){
		if(given_path[i]!=DFS_path[i]){
			cout << 0;
			return 0;
		}
	}
	cout << 1;
	
	
}

배열 대신 벡터로 동적으로 배열을 이용하면

메모리를 절약할 수 있겠지만 귀찮은 관계로 대부분 배열을 이용했다.

아마 인접리스트를 이용하지 않고 인접행렬[nxn]그래프를 이용하면 메모리 초과가 될 것이다.

인접리스트 알아보기

https://www.acmicpc.net/problem/2252

#include <bits/stdc++.h>
using namespace std;


int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n,m;
	cin >> n >> m;
	
	vector<int> graph[32001];
	vector<int> degree(n+1, 0);
	
	for(int i=0; i<m;i++){
		int a,b;
		cin >> a >> b;
		
		graph[a].push_back(b);
		degree[b]++;
	}
	
	queue<int> Q;
	
	
	for(int i=1; i<=n; i++){
		if(degree[i]==0) Q.push(i);
	}
	
	while(!Q.empty()){
		int cur = Q.front();
		Q.pop();
		cout << cur <<' ';
		
		for(int i=0; i<graph[cur].size(); i++){
			int nx = graph[cur][i];
			degree[nx]--;
			if(degree[nx]==0) Q.push(nx);	
		}
	}
		
	
}

처음에 아무 생각없이 32000x32000 벡터를 만들었다가

메모리 초과로 틀렸다.

그래서 32000행 벡터를 만들고 노드를 인풋 받을 때마다 push_back 해주었다.

처음엔 그래프 거리를 구하는 걸 냅색 알고리즘을 어떻게 응용해야할지 모르겠어서

우선순위큐 BFS를 이용해 풀어봤다.

답은 맞았다.

#include <bits/stdc++.h>
using namespace std;

int n, m;

int arr[101][101], ch[101];

struct Edge{
	int node, dist;
	Edge(int a, int b){
		node = a;
		dist = b;
	}
	bool operator<(const Edge &e) const{
		return dist > e.dist;
	}
	
};

priority_queue<Edge> Q;

int DIST(int s,int e){

	int res = INT_MAX;
	Q.push(Edge(s,0));
	
	while(!Q.empty()){
		int cur_node = Q.top().node;
		int cur_dist = Q.top().dist;
		Q.pop();
		ch[cur_node] = 1;
		if(cur_node == e){
			res = min(res, cur_dist);
		}
		
		for(int i=1; i<=n; i++){
			if(arr[cur_node][i]!=INT_MAX && ch[i]==0){
				Q.push(Edge(i, cur_dist+arr[cur_node][i]));
			}
		}
		
	}
	
	for(int i=1; i<=n; i++){
		ch[i] = 0;
	}
	
	
	return res;

}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> m;
	
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if(i==j) continue;
			arr[i][j] = INT_MAX;
		}
	}
	
	for(int i=1; i<=m; i++){
		int a,b,c;
		cin>> a >> b >> c;
		arr[a][b] = c;
	}

	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			int ans = DIST(i,j);
			if(ans==INT_MAX) cout <<"M ";
			else cout << ans << " ";
		}
		cout <<'\n';
	}
	
}

플로이드워샬 알고리즘이란?

플로이드워샬 알고리즘은 모든 정점에서 모든 정점으로 가는 최단 거리를 구하는 알고리즘이다.

다익스트라 벨만포드 알고리즘과 플로이드워샬 알고리즘의 차이는?

다익스트라, 벨만포드 알고리즘은 한 정점에서 다른 정점으로 가는 최단 거리를 구한다는 점에서

플로이드워샬 알고리즘과 차이가 있다.

점화식

arr[i][j] 는 i노드에서 j노드로 가는 거리를 저장한다.

arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);

i노드에서 j노드로 가는 거리와

i노드에서 k노드를 거쳐 j 노드를 가는 거리를 비교해서 더 짧은 방법을 선택한다.

k에 대하여 존재하는 모든 노드를 한 번씩 다 적용시켜보면

모든 노드에서 모든 노드로 가는 최단 거리 테이블을 만들 수 있다.

다음과 같은 그림이 있을 때

k노드를 선택하기 이전에

arr[i][j] = 20이었다.

i - > j 노드로 가는 것 보다

i -> k -> j 노드로 가는 게 더 짧다.

arr[i][j] = 18로 선택된다.

추가적으로 t 노드가 있을 때

이제 i ->k ->j 보다

i-> k -> t -> j 노드로 가는 게 더 빠르다.

arr[i][j] = 18에서

arr[i][j] = arr[i][t] + arr[t][j] = 17로 갱신된다.

이런식으로 모든 노드에 대해서 갱신해주면

모든 노드에서 모든 노드로 가는 최단 거리를 구할 수 있다.

arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);

k번째 노드를 계속 선택해줘서 경유점으로 둘 때

최솟값을 계속 갱신해준다는 점에서 냅색알고리즘과 유사하다.

노드를 가방에 담을지 안담을지 선택한다고 보면 된다.

for(int k=1; k<=n; k++){
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            if(arr[i][k]==INT_MAX || arr[k][j] == INT_MAX) continue;
            arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);
        }
    }
}

1부터 n까지 모든 노드 k에 대해서

k를 경유점으로 추가하는 것과 이전의 k를 경유점으로 추가하지 않는 것을 비교하면서

최솟값을 계속 저장해준다.

이러면 결과적으로 arr[i][j]에 i부터 j까지 가는 최단 거리가 저장된다.

(애초에 i에서 j로 갈 수 없는 점들은 INT_MAX로 초기화해두고 시작한다)

#include <bits/stdc++.h>
using namespace std;

int n, m;

int arr[101][101];


int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> m;
	
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if(i==j) continue;
			arr[i][j] = INT_MAX;
		}
	}
	
	for(int i=1; i<=m; i++){
		int a,b,c;
		cin>> a >> b >> c;
		arr[a][b] = c;
	}

	for(int k=1; k<=n; k++){
		for(int i=1; i<=n; i++){
			for(int j=1; j<=n; j++){
				if(arr[i][k]==INT_MAX || arr[k][j] == INT_MAX) continue;
				arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);
			}
		}
	}
	
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if (arr[i][j]==INT_MAX) cout << "M ";
			else cout << arr[i][j] << ' ';
		}
		cout << '\n';
	}
	
}

플로이드 와샬 알고리즘을 이용하면

맨위처럼 우선순위큐 BFS를 사용하지 않아도

간단하게 모든 노드에서 모든 노드로 가는 최단거리를 구할 수 있다.