https://www.acmicpc.net/problem/15684
15684번: 사다리 조작
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선
www.acmicpc.net
1.문제설명
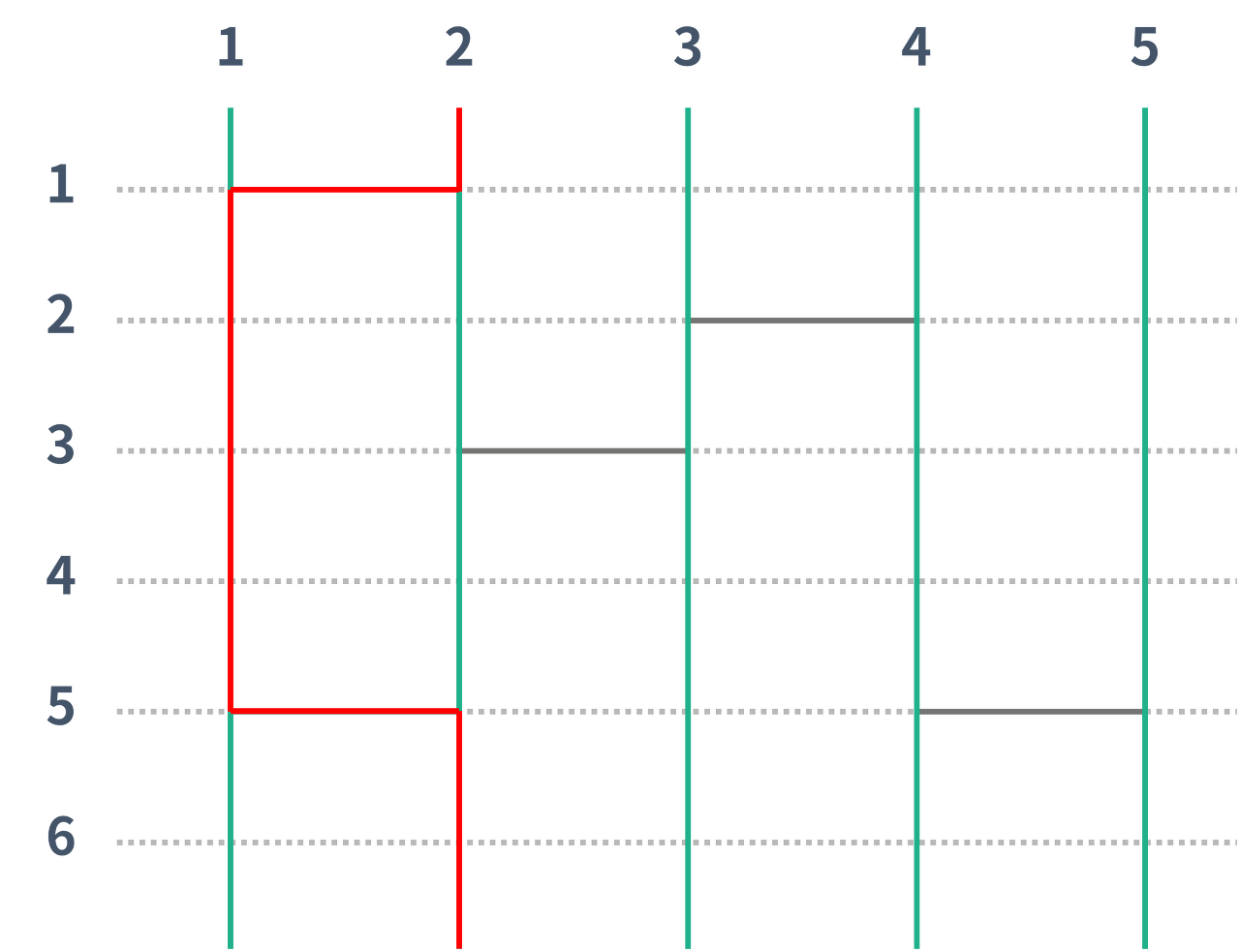
N*H의 사다리가 주어진다.
사다리게임의 결과로 모든 숫자에 대해 X번은 X를 갖도록
사다리 갯수를 추가해 조작해주어야 한다.
단 필요한 사다리 갯수가 3개를 초과하면 -1을 출력해준다.
2.접근 방법[알고리즘]
가로에 사다리가 없는 부분에 대하여 사다리를 추가해주었을 때 문제 조건을 맞는지 확인하면서
백트래킹을 돌아보면 된다. 이전의 백준 스도쿠 문제와 유사하다.
https://dingcoding.tistory.com/83
백준 2580번: 스도쿠 - DFS, 백트래킹 C++
https://www.acmicpc.net/problem/2580 2580번: 스도쿠 스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로,
dingcoding.tistory.com
다만 백트래킹을 돌면서 확인해야할 조건은 가로선이 연속되면 안된다.
그리고 가로선을 하나씩 선택해주면서 갯수가 3개를 넘어간다면 return 조건을 추가해
3개이상 도는 경우를 가지치기 해준다.
또한 가로선을 선택하는 것에 대하여 이전에 선택했던 걸 돌면서 다시 선택하면
불필요하게 중복적인 계산을 하므로 사다리를 선택하는 방법은 조합을 구하는 것처럼 생각해야 한다.
1번 2번 3번을 선택했으면, 3 2 1을 다시 선택하면 안된다는 얘기다.
DFS 함수에 매개변수를 잘 설정해주면 중복된 선택을 피할 수 있다.
3.문제풀이코드 C++
#include <bits/stdc++.h>
using namespace std;
//arr 배열에 true값으로 사다리 표시
int arr[40][40],n,m,h,ans=INT_MAX, target_cnt;
// 사다리타기 체크
bool check() {
for (int i = 1; i <= n; i++) {
int start = i;
for (int j = 1; j <= h; j++) {
if (start+1 <= n && arr[j][start] == true) {
start++;
}
else if (start-1 >=1 && arr[j][start-1] == true) {
start--;
}
}
if (start != i) return false;
}
return true;
}
void DFS(int h_cnt, int n_cnt, int cnt) {
// 사다리 선택하는 횟수를 통해 가지치기 하기
if (cnt == target_cnt) {
if (check()) {
ans = cnt;
}
return;
}
//매개변수 설정을 잘 해주면 이전에 돌았던 거 다시 안돌아도 되서
//가지치기를 할 수 있다.
for (int i = h_cnt; i <= h; i++, n_cnt = 1) {
for (int j = n_cnt; j < n; j++) {
//연속된 사다리 선택 피해주기
if (arr[i][j - 1] || arr[i][j] || arr[i][j + 1]) continue;
else {
arr[i][j] = 1;
DFS(i, j, cnt + 1);
arr[i][j] = 0;
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> h;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
arr[a][b] = true;
}
for (int i = 0; i <= 3; i++) {
target_cnt = i;
DFS(1, 1, 0);
if (ans != INT_MAX) {
cout << ans;
return 0;
}
}
cout << -1;
return 0;
}
이 문제에 대해 구글링을 해보다가 다소 특이한 코드인데
효율적인 방법을 발견했다.
for (int i = h_cnt; i <= h; i++, n_cnt = 1) {
for (int j = n_cnt; j < n; j++) {
//연속된 사다리 선택 피해주기
if (arr[i][j - 1] || arr[i][j] || arr[i][j + 1]) continue;
else {
arr[i][j] = 1;
DFS(i, j, cnt + 1);
arr[i][j] = 0;
}
}
}
초록색 부분의 좌표가 위 코드에서 [h_cnt, n_cnt] 라고 할 때
회색 부분이 지금까지 탐색한 부분이고, 흰색 부분이 앞으로 탐색해야할 부분이다.
단순하게 2중 for문을 사용하면 탐색했던 부분을 불필요하게 다시 탐색해야 한다.
하지만
for (int i = h_cnt; i <= h; i++, n_cnt = 1) {
for (int j = n_cnt; j < n; j++) {i++, n_cnt = 1 이렇게 초기화 하는 부분을 넣어주면
i for 문이 처음 돌 때는 j의 값이 n_cnt의 값 부터 돌고
이후에는 n_cnt ==1이 되어서 계속 돌아준다.
이렇게 해주면 흰색 부분만 탐색해줄 수 있다.
불필요한 탐색을 줄여주기 위해 백트래킹, DFS의 매개변수와 같이 사용하면
상당히 편할 것 같다.
시간초과로 틀린 이유 - 틀린코드
#include <bits/stdc++.h>
using namespace std;
//arr 배열에 true값으로 사다리 표시
int arr[40][40],n,m,h,ans=INT_MAX;
// 사다리타기 체크
bool check() {
for (int i = 1; i <= n; i++) {
int start = i;
for (int j = 1; j <= h; j++) {
if (start+1 <= n && arr[j][start] == true) {
start++;
}
else if (start-1 >=1 && arr[j][start-1] == true) {
start--;
}
}
if (start != i) return false;
}
return true;
}
void DFS(int c) {
if (c > 3) {
return;
}
if (check()) {
ans = min(c,ans);
return;
}
else {
for (int i = 1; i <= h; i++) {
for (int j = 1; j < n; j++) {
// 이 부분에서 2중포문을 돌면서 DFS를 하면
// DFS를 계속 돌면서 이전에 돌았던 걸 다시 돌게 되어 시간낭비가 발생한다.
if (arr[i][j-1] || arr[i][j] || arr[i][j+1]) continue;
else {
arr[i][j] = 1;
DFS(c + 1);
arr[i][j] = 0;
}
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> h;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
arr[a][b] = true;
}
DFS(0);
if (ans <= 3) {
cout << ans << '\n';
}
else {
cout << -1 << '\n';
}
return 0;
}

시간이 많이 걸려서 여러번 다시 풀어 봤다.
DFS에서 중복된 선택을 피하기 위해 가지치기를 어떻게 할 지 잘 생각해야 시간을 줄일 수 있다.
'Algorithm > problem' 카테고리의 다른 글
| 백준 13913번: 숨바꼭질 4 - BFS, DFS 활용 (0) | 2022.02.02 |
|---|---|
| 백준 13459번 : 구슬 탈출 - BFS C++ 문제풀이코드 (0) | 2022.02.02 |
| 백준 14889번: 스타트와 링크 - DFS, 백트래킹, 조합 C++ (0) | 2022.01.30 |
| 백준 2580번: 스도쿠 - DFS, 백트래킹 C++ (2) | 2022.01.30 |
| 백준 1987번: 알파벳 - DFS, 백트래킹 C++ (0) | 2022.01.30 |