처음엔 그래프 거리를 구하는 걸 냅색 알고리즘을 어떻게 응용해야할지 모르겠어서
우선순위큐 BFS를 이용해 풀어봤다.
답은 맞았다.
#include <bits/stdc++.h>
using namespace std;
int n, m;
int arr[101][101], ch[101];
struct Edge{
int node, dist;
Edge(int a, int b){
node = a;
dist = b;
}
bool operator<(const Edge &e) const{
return dist > e.dist;
}
};
priority_queue<Edge> Q;
int DIST(int s,int e){
int res = INT_MAX;
Q.push(Edge(s,0));
while(!Q.empty()){
int cur_node = Q.top().node;
int cur_dist = Q.top().dist;
Q.pop();
ch[cur_node] = 1;
if(cur_node == e){
res = min(res, cur_dist);
}
for(int i=1; i<=n; i++){
if(arr[cur_node][i]!=INT_MAX && ch[i]==0){
Q.push(Edge(i, cur_dist+arr[cur_node][i]));
}
}
}
for(int i=1; i<=n; i++){
ch[i] = 0;
}
return res;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(i==j) continue;
arr[i][j] = INT_MAX;
}
}
for(int i=1; i<=m; i++){
int a,b,c;
cin>> a >> b >> c;
arr[a][b] = c;
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
int ans = DIST(i,j);
if(ans==INT_MAX) cout <<"M ";
else cout << ans << " ";
}
cout <<'\n';
}
}
플로이드워샬 알고리즘이란?
플로이드워샬 알고리즘은 모든 정점에서 모든 정점으로 가는 최단 거리를 구하는 알고리즘이다.
다익스트라 벨만포드 알고리즘과 플로이드워샬 알고리즘의 차이는?
다익스트라, 벨만포드 알고리즘은 한 정점에서 다른 정점으로 가는 최단 거리를 구한다는 점에서
플로이드워샬 알고리즘과 차이가 있다.
점화식
arr[i][j] 는 i노드에서 j노드로 가는 거리를 저장한다.
arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);i노드에서 j노드로 가는 거리와
i노드에서 k노드를 거쳐 j 노드를 가는 거리를 비교해서 더 짧은 방법을 선택한다.
k에 대하여 존재하는 모든 노드를 한 번씩 다 적용시켜보면
모든 노드에서 모든 노드로 가는 최단 거리 테이블을 만들 수 있다.
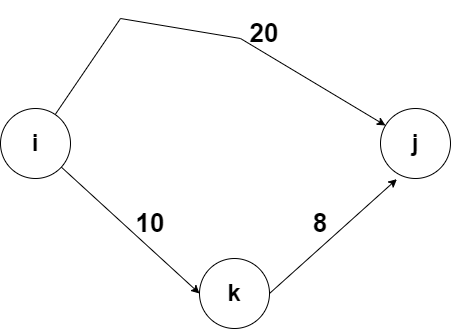
다음과 같은 그림이 있을 때
k노드를 선택하기 이전에
arr[i][j] = 20이었다.
i - > j 노드로 가는 것 보다
i -> k -> j 노드로 가는 게 더 짧다.
arr[i][j] = 18로 선택된다.
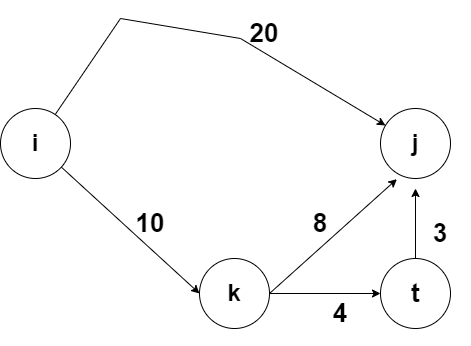
추가적으로 t 노드가 있을 때
이제 i ->k ->j 보다
i-> k -> t -> j 노드로 가는 게 더 빠르다.
arr[i][j] = 18에서
arr[i][j] = arr[i][t] + arr[t][j] = 17로 갱신된다.
이런식으로 모든 노드에 대해서 갱신해주면
모든 노드에서 모든 노드로 가는 최단 거리를 구할 수 있다.
arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);
k번째 노드를 계속 선택해줘서 경유점으로 둘 때
최솟값을 계속 갱신해준다는 점에서 냅색알고리즘과 유사하다.
노드를 가방에 담을지 안담을지 선택한다고 보면 된다.
for(int k=1; k<=n; k++){
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(arr[i][k]==INT_MAX || arr[k][j] == INT_MAX) continue;
arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);
}
}
}1부터 n까지 모든 노드 k에 대해서
k를 경유점으로 추가하는 것과 이전의 k를 경유점으로 추가하지 않는 것을 비교하면서
최솟값을 계속 저장해준다.
이러면 결과적으로 arr[i][j]에 i부터 j까지 가는 최단 거리가 저장된다.
(애초에 i에서 j로 갈 수 없는 점들은 INT_MAX로 초기화해두고 시작한다)
#include <bits/stdc++.h>
using namespace std;
int n, m;
int arr[101][101];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(i==j) continue;
arr[i][j] = INT_MAX;
}
}
for(int i=1; i<=m; i++){
int a,b,c;
cin>> a >> b >> c;
arr[a][b] = c;
}
for(int k=1; k<=n; k++){
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(arr[i][k]==INT_MAX || arr[k][j] == INT_MAX) continue;
arr[i][j] = min(arr[i][j], arr[i][k]+arr[k][j]);
}
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if (arr[i][j]==INT_MAX) cout << "M ";
else cout << arr[i][j] << ' ';
}
cout << '\n';
}
}플로이드 와샬 알고리즘을 이용하면
맨위처럼 우선순위큐 BFS를 사용하지 않아도
간단하게 모든 노드에서 모든 노드로 가는 최단거리를 구할 수 있다.
'Algorithm > etc' 카테고리의 다른 글
| cycle 찾기 (0) | 2022.02.21 |
|---|---|
| Segment Tree 구현 코드 C++ (0) | 2022.02.11 |
| 냅색 알고리즘(한번 만 사용가능) 2차원, 1차원 배열 (0) | 2022.01.26 |
| 냅색 문제 (0) | 2022.01.26 |
| LIS 최대 부분 증가수열 - DP (0) | 2022.01.25 |