https://www.acmicpc.net/problem/1854

1.문제설명

1번 노드에서 출발하여 다른 모든 노드까지의 K번째 최단 거리를 찾는 문제이다.

일반적으로

한 노드에서 다른 모든 노드까지의 최단 거리를 구할 때 다익스트라 알고리즘을 이용한다.

이 문제도 다익스트라 알고리즘을 응용하면 K번째 최단거리를 구할 수 있다.

2.접근방법[알고리즘]

이 문제에서 가장 헷갈리는 점은 

기존 최단거리를 구하는 다익스트라 알고리즘과 다르게

방문한 노드를 재방문해도 된다는 점이다.

방문한 노드를 재방문해도 되도록 코드를 구성하면

계속 무한루프에 빠지지 않을까?

이를 해결하기 위해 

방문 여부 대신 다른 조건을 추가해주어야 한다.

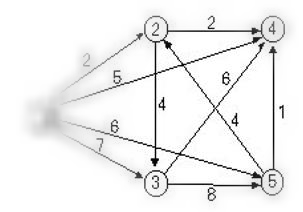
그림에 잘 보면 2->3->5->2가 계속 무한으로 순환할 수 있다.

노드를 방문하는 우선순위큐와 다르게

특정 노드까지 거리를 저장하는 우선순위큐 배열을 따로 두어서

K번째 최단 거리까지 구했다면 더 이상 순환하지 않도록 코드를 구현해야 한다.

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;

int n, m, k;
struct Edge {
	int x;
	long long val;
	bool operator<(const Edge& b) const {
		return val > b.val;
	}
};

vector<pair<int, int> > graph[1001];
priority_queue<int> Node[1001];
priority_queue<Edge> Q;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> m >> k;

	for (int i = 0; i < m; i++) {
		int a, b, c;
		cin >> a >> b >> c;
		graph[a].push_back({ b,c });
	}

	Node[1].push(0);
	Q.push({ 1,0 });

	while (!Q.empty()) {
		int x = Q.top().x;
		int val = Q.top().val;
		Q.pop();

		for (int i = 0; i < graph[x].size(); i++) {
			int nx = graph[x][i].first;
			int nd = graph[x][i].second + val;

			if (Node[nx].size() < k) {
				Node[nx].push(nd);
				Q.push({ nx,nd });
			}
			else {
				if (Node[nx].top() > nd) {
					Node[nx].pop();
					Node[nx].push(nd);
					Q.push({ nx,nd });
				}
			}
		}
	}

	for (int i = 1; i <= n; i++) {
		if (Node[i].size() < k) {
			cout << -1 << '\n';
		}
		else {
			cout << Node[i].top() << '\n';
		}
	}


	return 0;
}

https://www.acmicpc.net/problem/1507

1.문제설명

INPUT

5
0 6 15 2 6
6 0 9 8 12
15 9 0 16 18
2 8 16 0 4
6 12 18 4 0

OUTPUT

55

문제에서 N개의 노드가 있을 때

노드에서 노드로 가는 모든 최단 거리를 INPUT으로 준다.

주어진 노드간 최단 거리를 유지하면서 간선의 개수를 최소로 할 때 

간선의 거리의 합을 구해야 한다.

2.접근방법[알고리즘]

주어진 인풋을 dist배열에 넣고

플로이드 워셜을 한번 실행했을 때

dist[i][k] + dist[k][j]) == dist[i][j]

이런 상황이 있으면 간선을 최소로 하기위해

dist[i][j] 의 간선을 사용하지 않고

dist[i][k] 와 dist[k][j]의 간선만 사용하면 된다.

맨 처음엔 문제에서 주어진 인풋의 간선을 모두 사용하는 걸 전제로 하고

위와 같은 간선이 있으면 i - j 를 이어주는 간선을 없애주면

최소 간선을 구해낼 수 있다.

for (int k = 0; k < n; k++) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (i == j || j == k || i == k) continue;
				if ((dist[i][k] + dist[k][j]) == dist[i][j]) {
					arr[i][j] = INF;
				}
				else if (dist[i][k] + dist[k][j] < dist[i][j]) {
					cout << -1 << '\n';
					return 0;
				}
			}
		}
	}

3. 문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;


const int INF = 0x3f3f3f3f;

int n, arr[21][21];

int dist[21][21];
bool ch[21][21];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	memset(dist, 0x3f, sizeof(dist));

	cin >> n;

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> arr[i][j];
			dist[i][j] = min(dist[i][j], arr[i][j]);
		}
	}

	for (int k = 0; k < n; k++) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (i == j || j == k || i == k) continue;
				if ((dist[i][k] + dist[k][j]) == dist[i][j]) {
					arr[i][j] = INF;
				}
				else if (dist[i][k] + dist[k][j] < dist[i][j]) {
					cout << -1 << '\n';
					return 0;
				}
			}
		}
	}

	int sum = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (arr[i][j] < INF) sum += arr[i][j];
		}
	}

	cout << sum / 2 << '\n';



	return 0;
}

https://www.acmicpc.net/problem/1956

플로이드 와샬 알고리즘을 이용해 풀고

거리의 최대치와 INT StackOverflow를 유의해서 풀어야한다.

#include <bits/stdc++.h>
using namespace std;

const int INF = 2e9;
int n,m, dist[401][401];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	fill(&dist[0][0], &dist[400][401], INF);

	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		int a, b, c;
		cin >> a >> b >> c;
		dist[a][b] = c;
	}

	for (int k = 1; k <= n; k++) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				if (dist[i][k] >= INF || dist[k][j] >= INF) continue;
				dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
			}
		}
	}

	int ans = INT_MAX;
	for (int i = 1; i <= n; i++) {
		ans = min(dist[i][i], ans);
	}

	if (ans == INF) {
		cout << -1 << '\n';
	}
	else {
		cout << ans << '\n';
	}
	return 0;
}

https://www.acmicpc.net/problem/2458

1.문제설명

서로 키를 비교한 결과를 입력으로 주었을 때

키의 순서를 알 수있는 노드가 몇 개인지 구하는 문제이다.

2.접근방법

해당 노드의 키 순서를 알려면

해당 노드를 제외한 모든 노드와 비교가 되어야 한다.

플로이드 와샬 알고리즘으로 모든 노드간 거리를 구했을 때

만약 거리[a][b] 와 거리[b][a]가 모두 비교가 되지 않은 채 INF 값이 있다면

 a와 b는 순서를 알 수 없다.

3.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;



int n, m, dist[501][501];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	memset(dist, 0x3f, sizeof(dist));

	cin >> n >> m;

	for (int i = 1; i <= n; i++) {
		dist[i][i] = 0;
	}

	for (int i = 0; i < m; i++) {
		int a, b;
		cin >> a >> b;
		dist[a][b] = 1;
	}


	for (int k = 1; k <= n; k++) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
			}
		}
	}

	int ans = 0;
	for (int i = 1; i <= n; i++) {

		bool canKnow = true;
		for (int j = 1; j <= n; j++) {
			if (dist[i][j] > 10000) {
				if (dist[j][i] > 10000) {
					canKnow = false;
				}

			}
		}

		if (canKnow) ans++;

	}
	cout << ans << '\n';


	return 0;
}

https://www.acmicpc.net/problem/2610

#include <bits/stdc++.h>
using namespace std;


int n,k;
int dist[101][101];
bool grouped[101];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	memset(dist, 0x3f, sizeof(dist));

	cin >> n >> k;

	for (int i = 0; i < k; i++) {
		int a, b;
		cin >> a >> b;
		dist[a][b] = 1;
		dist[b][a] = 1;
	}

	for (int i = 1; i <= n; i++) {
		dist[i][i] = 0;
	}

	for (int k = 1; k <= n; k++) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
			}
		}
	}
	
	int cnt = 0;

	vector<int> king;

	for (int i = 1; i <= n; i++) {
		vector<int> g;
		for (int j = 1; j <= n; j++) {
			if (dist[i][j] < 200 && grouped[j] == false) {
				grouped[j] = true;
				g.push_back(j);
			}
		}
		
		if (g.size() > 0) {
			cnt++;

			int minn = INT_MAX;
			int midx = -1;

			for (int j = 0; j < g.size(); j++) {

				int maxx = 0;
				for (int k = 0; k < g.size(); k++) {
					maxx = max(maxx, dist[g[j]][g[k]]);
				}
				if (maxx < minn) {
					minn = maxx;
					midx = g[j];
				}
			}
			king.push_back(midx);
		}
	}

	sort(king.begin(), king.end());

	cout << cnt << '\n';
	for (int i = 0; i < king.size(); i++) {
		cout << king[i] << '\n';
	}

	return 0;
}

https://www.acmicpc.net/problem/8983

#include <bits/stdc++.h>
using namespace std;

vector<int> gun;


bool distance(int x, int y, int L) {

	bool ans = false;
	if (y > L) return false;

	int s = 0;
	int e = gun.size() - 1;

	while (s <= e) {

		int mid = (s + e) / 2;

		if (abs(gun[mid] - x) + y <=L) {
			ans = true;
			break;
		}
		else if (gun[mid] > x) {
			e = mid - 1;
		}
		else {
			s = mid + 1;
		}
	}


	return ans;
}


int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	int m, n, l;
	cin >> m >> n >> l;
	

	for (int i = 0; i < m; i++) {
		int tmp;
		cin >> tmp;
		gun.push_back(tmp);
	}

	sort(gun.begin(), gun.end());

	int cnt = 0;
	for (int i = 0; i < n; i++) {
		int x, y;
		cin >> x >> y;
		if (distance(x, y ,l)) cnt++;
	}

	cout << cnt << '\n';


	

	return 0;
}

https://www.acmicpc.net/problem/6087

#include <bits/stdc++.h>
using namespace std;

int w, h;
int stx, sty, enx, eny;
int arr[101][101];
int dis[101][101];

int dx[4] = { -1, 0,1,0 };
int dy[4] = { 0, 1,0,-1 };

struct Node {
	int x, y, dist, direction;

	bool operator<(const Node& b) const {
		return dist > b.dist;
	}
};



int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	memset(dis, 0x3f, sizeof(dis));

	cin >> w >> h;
	bool st = false;

	for (int i = 0; i < h; i++) {
		string s;
		cin >> s;
		for (int j = 0; j < w; j++) {
			if (s[j] == '*') {
				arr[i][j] = -1;
			}
			else if (s[j] == 'C' && st == false) {
				stx = i;
				sty = j;
				st = true;
			}
			else if (s[j] == 'C' && st == true) {
				enx = i;
				eny = j;
			}
		}
	}


	priority_queue<Node> Q;

	dis[stx][sty] = 0;

	for (int i = 0; i < 4; i++) {
		int nx = stx + dx[i];
		int ny = sty + dy[i];

		if (nx < 0 || nx >= h || ny < 0 || ny >= w || arr[nx][ny]==-1 ) continue;

		Q.push({ nx,ny,0,i });
	}


	while (!Q.empty()) {
		int x = Q.top().x;
		int y = Q.top().y;
		int dist = Q.top().dist;
		int direction = Q.top().direction;
		Q.pop();


		if (dis[x][y] < dist) continue;
		dis[x][y] = dist;

		if (x == enx && y == eny) {
			cout << dist << '\n';
			return 0;
		}

		for (int i = 0; i < 4; i++) {
			if (abs(i - direction) == 2) continue;

			int nx = x + dx[i];
			int ny = y + dy[i];
			int nd = dist;
			if (i != direction) {
				nd++;
			}
			if (nx < 0 || nx >= h || ny < 0 || ny >= w || arr[nx][ny] == -1) continue;
			if (dis[nx][ny] < nd) continue;
			Q.push({ nx,ny,nd,i });
		}
	}



	//for (int i = 0; i < h; i++) {
	//	for (int j = 0; j < w; j++) {
	//		if (dis[i][j] > 10) cout << '*';
	//		else cout << dis[i][j];
	//	}
	//	cout << '\n';
	//}


	return 0;
}

https://www.acmicpc.net/problem/2108

#include <bits/stdc++.h>
using namespace std;

struct Count {
	int x, cnt;

	bool operator<(const Count& b) const {
		if (cnt == b.cnt) {
			return x < b.x;
		}
		return cnt > b.cnt;
	}
};

int arr[9000];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n;
	vector<int> v;

	cin >> n;
	int sum = 0;
	for (int i = 0; i < n; i++) {
		int tmp;
		cin >> tmp;
		sum += tmp;

		arr[tmp + 4000]++;
		v.push_back(tmp);
	}

	sort(v.begin(), v.end());

	vector<Count> freq;

	for (int i = 0; i < 9000; i++) {
		if (arr[i] > 0) {
			freq.push_back({ i,arr[i] });
		}
	}

	sort(freq.begin(), freq.end());

	int freq_ans = freq[0].x - 4000;
	if (freq.size() >= 2 && freq[0].cnt == freq[1].cnt) {
		freq_ans = freq[1].x - 4000;
	}
	

	double mean = sum / (double)n;

	int mm;
	if (mean >= 0) {
		mm = int(mean + 0.5);
	}
	else {
		mm = int(mean - 0.5);
	}

	cout << mm << '\n';
	cout << v[n / 2] << '\n';

	cout << freq_ans << '\n';

	cout << v[v.size() - 1] - v[0] << '\n';
	
	return 0;
}