https://www.acmicpc.net/problem/1949

1. 문제설명

인접한 노드 두개가 우수마을이 되면 안된다.

그리고 자신이 우수마을이 아니라면 인접한 노드 중 적어도 하나가 우수마을이 되어야한다.

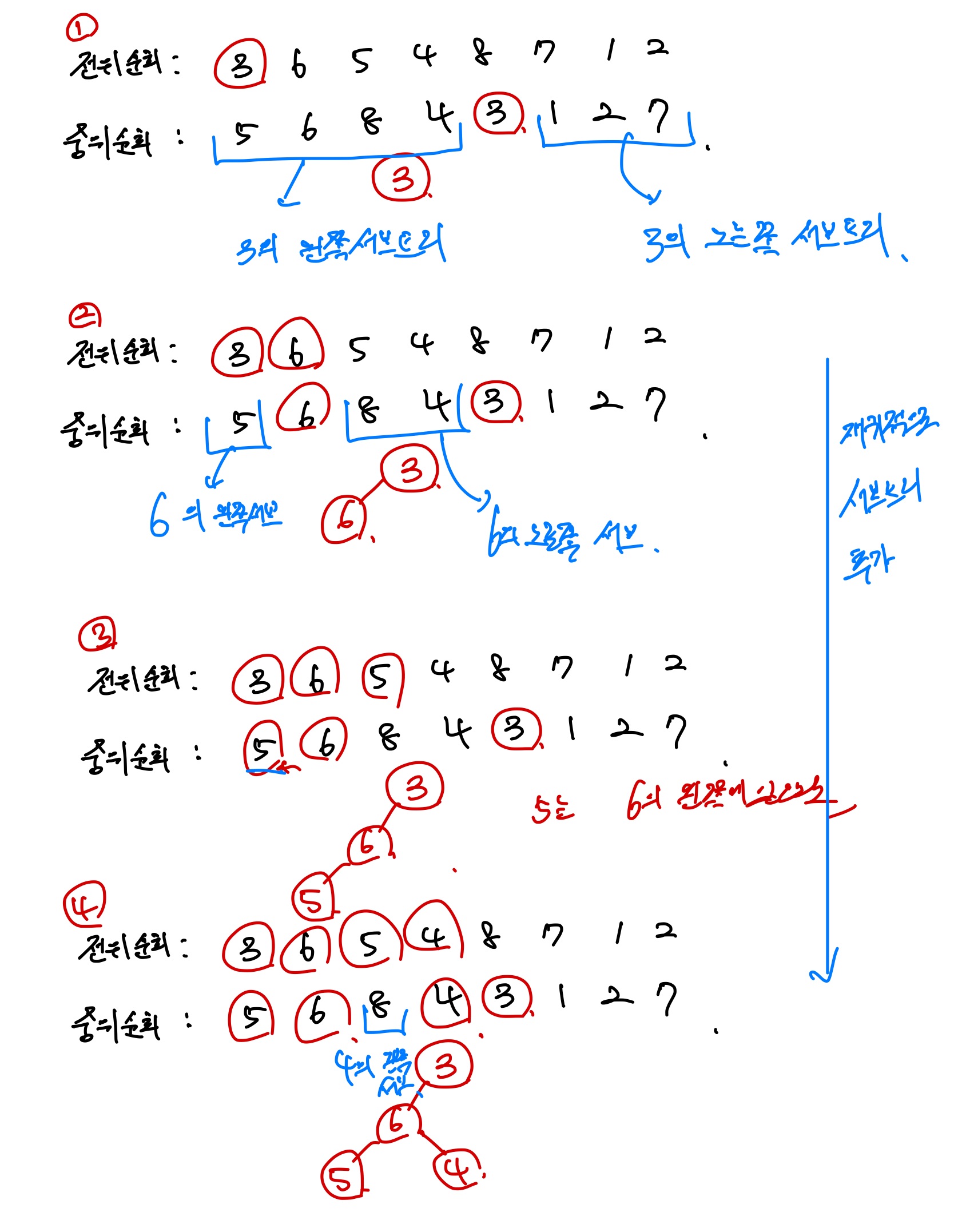
문제를 해결하기 위해

노드를 재귀적으로 탐색해야한다.

현재 노드가 우수마을인 경우와 우수마을이 아닌 경우를 나눈다.

그리고 현재 노드가 우수마을인 경우에는 다음 노드는 무조건 우수마을이면 안된다.

현재 노드가 우수마을이 아닌 경우에는 다음 노드는 우수마을이거나 우수마을이 아닐 수 있다.

이 때

현재 우수마을이 아닌데 다음 마을도 우수마을이 아닌 경우 문제가 생길 수 있다고 생각했다.

예를 들어 세개의 노드가 다 우수마을이 아닌 경우라면 문제의 조건에 맞지 않다.

하지만 다음 코드와 같이 재귀적으로 탐색하면서 최댓값을 계속 넘겨주다보면

모든 마을이 우수마을이 아닌 경우는 남지 않아서 괜찮다.

최댓값만 남기기 때문에 모든 마을이 우수마을이 아닌 경우는 살아남을 수 없다.

2.문제풀이코드 C++

#include <bits/stdc++.h>
using namespace std;
#define MX 10001

int N, people[MX], dp[MX][2];
bool vis[MX];
vector<int> adj[MX];

void DFS(int node){
    dp[node][0] = 0;
    dp[node][1] = people[node];
    vis[node] = 1;

    for(int i=0; i<adj[node].size(); i++){
        int nx = adj[node][i];
        if(vis[nx]) continue;

        DFS(nx);
        dp[node][0] += max(dp[nx][0], dp[nx][1]);
        dp[node][1] += dp[nx][0];
    }
}


int main() {
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> N;
    for(int i=1; i<=N; i++){
        cin >> people[i];
    }

    for(int i=1; i<N; i++){
        int a, b;
        cin >> a >> b;
        adj[a].push_back(b);
        adj[b].push_back(a);
    }

    DFS(1);
    cout << max(dp[1][0], dp[1][1]) << '\n';
    return 0;
}

https://www.acmicpc.net/problem/4256

1. 문제설명

트리의 전위순회 결과와 중위순회 결과를 바탕으로 트리의 구조를 구해낼 수 있고,

이를 후위순회한 결과를 출력하는 문제이다.

전위 순회한 결과 먼저오는 노드가 루트노드임을 알 수 있고,

그 루트노드를 바탕으로 중위순회 결과를 보면

해당 루트노드의 왼쪽 서브트리와 오른쪽 서브트리를 알 수 있다.

이를 재귀적으로 구현하면 트리 구조를 구현할 수 있고,

이를 후위순회하면  정답이 된다.

2. 문제풀이코드

#include <bits/stdc++.h>
using namespace std;

int n,pidx, preOrderRes[1001], inOrderRes[1001], order[1001];

struct Node{
    int data;
    Node* left = nullptr;
    Node* right = nullptr;
    Node(int _data, Node* _left, Node* _right): data(_data), left(_left), right(_right){}
};


void postOrder(Node* root){
    if(root== nullptr) return;
    postOrder(root->left);
    postOrder(root->right);
    cout << root->data << ' ';
}

void deconstruct(Node* root){
    if(root == nullptr) return;
    deconstruct(root->left);
    deconstruct(root->right);
    root = nullptr;
    delete root;
}


Node* makeTree(int start, int end){
    if(start > end) return nullptr;
    
    Node* newNode = new Node(preOrderRes[pidx++], nullptr, nullptr);
    if(start==end) return newNode;
    int mid = order[newNode->data];
    newNode->left = makeTree(start, mid-1);
    newNode->right = makeTree(mid+1, end);
    return newNode;
}

void makeTree(Node** root){
    pidx = 1;
    *root = makeTree(1, n);
}



int main() {
    ios::sync_with_stdio(0); cin.tie(0);

    int t;
    cin >> t;
    for(int T=0; T<t; T++){
        cin >> n;
        for(int i=1; i<=n; i++){
            cin >> preOrderRes[i];
        }
        for(int i=1; i<=n; i++){
            cin >> inOrderRes[i];
            order[inOrderRes[i]] = i;
        }
        Node *root = nullptr;

        makeTree(&root);
        postOrder(root);
        cout << '\n';
        deconstruct(root);
    }

    return 0;
}

https://www.acmicpc.net/problem/5639

#include <bits/stdc++.h>
using namespace std;

struct Node{
    int data;
    Node* left;
    Node* right;

    Node(int _data, Node* _left, Node* _right): data(_data), left(_left), right(_right){};
};


void insert(Node** root,int value){
    Node* p = *root, *q = nullptr;

    while(p != nullptr){
        q = p;
        if(value < p->data){
            p = p->left;
        }
        else p = p->right;
    }

    Node* newNode = new Node(value, nullptr, nullptr);
    if(q == nullptr){
        *root = newNode;
    }
    else if(value < q->data){
        q->left = newNode;
    }
    else{
        q->right = newNode;
    }
}


void postOrder(Node* root){
    if(root== nullptr) return;
    postOrder(root->left);
    postOrder(root->right);
    cout << root->data << '\n';
}


int main() {
    ios::sync_with_stdio(0); cin.tie(0);

    int num;
    Node* root = nullptr;
    while(cin >> num){
        insert(&root, num);
    }
    postOrder(root);

    return 0;
}

https://www.acmicpc.net/problem/2250

#include <bits/stdc++.h>
using namespace std;
const int MX = 10003;

int column[MX] , N, root , order, totalLev;
int adj[MX][2], revAdj[MX][2];
vector<int> level[MX];


//root 노드 찾기
int findRoot(int node){
    bool ch[N+1];
    memset(ch, 0 , sizeof(ch));
    queue<int> Q;

    ch[node] = 1;
    Q.push(node);
    while(!Q.empty()){
        int cur = Q.front(); Q.pop();
        if(revAdj[cur][0] == 0 && revAdj[cur][1] == 0){
            return cur;
        }

        for(int i=0; i<2; i++){
            int nxt = revAdj[cur][i];
            if(nxt == 0 || nxt == -1) continue;

            if(!ch[nxt]){
                ch[nxt] = 1;
                Q.push(nxt);
            }
        }
    }
    return -1;
}

void getLevel(int node){
    bool ch[N+1];
    memset(ch, 0 , sizeof(ch));

    queue<int> Q;

    ch[node] = 1;
    Q.push(node);

    while(!Q.empty()) {
        int curSize = Q.size();
        totalLev++;
        for(int i=0; i<curSize; i++){
            int cur = Q.front(); Q.pop();
            level[totalLev].push_back(cur);

            for(int j=0; j<2; j++){
                int nxt = adj[cur][j];
                if(nxt == 0 || nxt == -1) continue;
                if(!ch[nxt]){
                    ch[nxt] = 1;
                    Q.push(nxt);
                }
            }
        }
    }
}


void inOrder(int node){
    if(node == -1) return;
    inOrder(adj[node][0]);
    column[node] = ++order;
    inOrder(adj[node][1]);
}


int main() {
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> N;

    for(int i=0; i<N; i++){
        int a, b, c;
        cin >> a >> b >> c;
        adj[a][0] = b;
        adj[a][1] = c;

        revAdj[b][0] = a;
        revAdj[c][1] = a;
    }

    root = findRoot(N);

    getLevel(root);
    inOrder(root);

    int ansLev = 0, ansWidth = 0;

    for(int i=1; i<=totalLev; i++){
        int minn = 10003, maxx = -1;

        for(auto num : level[i]){
            minn = min(column[num], minn);
            maxx = max(column[num], maxx);
        }

        int curWidth = maxx - minn + 1;

        if(curWidth > ansWidth){
            ansWidth = curWidth;
            ansLev = i;
        }
    }
    
    cout << ansLev << ' ' << ansWidth <<'\n';




    return 0;
}

https://www.acmicpc.net/problem/5670

1. 문제설명

휴대폰 자판을 입력할 때 자동완성기능이 존재하면,

특정 단어를 입력하기 위해서 자판을 몇번 눌러야 하는지 계산하는 문제이다.

단어 리스트가 주어지고, 각 단어마다 몇번 눌러야하는지 구하는 과정에서

트라이 알고리즘을 이용해야 문제를 시간내에 해결할 수 있다.

주어진 단어로 위와 같이 트리를 미리 구현하고

분기점과 단어가 끝나는 지점마다 카운트해주어야

하나의 단어를 입력하기 위해 자판을 몇번 입력해야하는지 알아낼 수 있다.

2. 문제풀이코드 C++

#include <bits/stdc++.h>
#define ALPHABETS 26
using namespace std;


const int ROOT = 1;
int unused = 2;
const int MX = 1000'003;
int nxt[MX][26];
bool chk[MX];
int childs[MX];

int ctoi(char c){
    return c-'a';
}

void insert(string &s){
    int cur = ROOT;
    for(auto c : s){
        if(nxt[cur][ctoi(c)] == -1){
            childs[cur]++;
            nxt[cur][ctoi(c)] = unused++;
        }
        cur = nxt[cur][ctoi(c)];
    }
    chk[cur] = true;
}


int count(string &s){
    int res = 1;

    int cur = ROOT;
    for(int i=0; i<s.length();i++){
        cur = nxt[cur][ctoi(s[i])];

        if(i!=s.length()-1 && (childs[cur] > 1||chk[cur])){
            res++;
        }
    }
    return res;
}


vector<string> words;



int n;

int main() {
    ios::sync_with_stdio(0); cin.tie(0);
    while(cin >> n){
        words.clear();
        unused = 2;

        fill(childs, childs+MX , 0);
        fill(chk, chk+MX, 0);
        for(int i=0; i<MX; i++){
            fill(nxt[i], nxt[i]+26, -1);
        }

        for(int i=0; i<n; i++){
            string s;
            cin >> s;
            insert(s);
            words.push_back(s);
        }


        double sum = 0;
        for(auto s : words){
//            cout << s << '\n';
//            cout << count(s) << '\n';
            sum += count(s);
        }


        cout << fixed;
        cout.precision(2);
        cout << sum / n << '\n';



    }

    return 0;
}

#include <stdio.h>
#include <stdlib.h>

struct node {
    int data;
    struct node *left;
    struct node *right;
} Node;

// 데이터 삽입(recursion)
void insert(struct node **root, int data) {
    struct node* ptr;
    struct node* newNode = (struct node*)malloc(sizeof(struct node));
    newNode->data = data;
    newNode->left = newNode->right = NULL;

    if(*root == NULL){
        *root = newNode;
        return;
    }

    ptr = *root;

    while(ptr){
        if(data < ptr->data){
            if(ptr->left == NULL){
                ptr->left = newNode;
                return;
            }
            else{
                ptr = ptr->left;
            }
        }
        else{
            if(ptr->right == NULL){
                ptr->right = newNode;
                return;
            }
            else{
                ptr = ptr->right;
            }
        }
    }
}

// 전위(preorder)탐색(recursion)
void preOrder(struct node *root) {
    if(root == NULL) return;
    printf("%d ", root->data);
    preOrder(root->left);
    preOrder(root->right);
}

// 중위(inorder)탐색(recursion)
void inOrder(struct node *root) {
    if(root == NULL) return;
    inOrder(root->left);
    printf("%d ", root->data);
    inOrder(root->right);
}

// 후위(postorder)탐색(recursion)
void postOrder(struct node *root) {
    if(root == NULL) return;
    postOrder(root->left);
    postOrder(root->right);
    printf("%d ", root->data);
}

// 노드의 개수(recursion)
int size(struct node *root) {
    if(root == NULL) return 0;
    return 1 + size(root->left) + size(root->right);
}

// 높이(recursion)
int height(struct node *root) {
    if(root == NULL) return 0;
    if(root->left == NULL && root->right == NULL) return 0;

    int leftHeight = height(root->left);
    int rightHeight = height(root->right);
    return 1 + (leftHeight>= rightHeight ? leftHeight : rightHeight);
}

// 미러 이미지로 변환하기(recursion)
void mirror(struct node **root) {
    if(*root == NULL) return;
    mirror(&(*root)->left);
    mirror(&(*root)->right);
    struct node *tmp = (*root)->left;
    (*root)->left = (*root)->right;
    (*root)->right = tmp;
}

// 노드에 저장된 데이터의 값의 합 구하기(recursion)
int sumOfWeight(struct node *root) {
    if(root == NULL) return 0;
    return sumOfWeight(root->left) + sumOfWeight(root->right) + root->data;
}

// 루트노드부터 단말노드까지의 경로 상의 데이터의 최대합(recusrion)
int maxPathWeight(struct node *root) {
    if(root == NULL) return 0;
    int leftWeight, rightWeight;
    leftWeight = maxPathWeight(root->left);
    rightWeight = maxPathWeight(root->right);
    return root->data + (leftWeight>=rightWeight ? leftWeight : rightWeight);
}

// 트리노드의 동적 메모리 해제하기(recursion)
void destruct(struct node **root) {
    if(*root == NULL) return;
    destruct(&((*root)->left));
    destruct(&((*root)->right));
    free(*root);
    *root = NULL;
}

재귀란

int factorial(int n){
	if (n==1) return 1
    return n * factorial(n-1);
}

재귀란 특정 함수나 개체를 설명할 때

그 함수나 개체를 바탕으로 설명하는 것을 의미한다.

특정 문제에 대해서 재귀를 이용하면 단순 반복문으로 해결하기 어려운 문제를 쉽고 간결하게 해결할 수 있다.

단 재귀를 이용해서 문제를 해결할 때는

stack Overflow가 발생하는 것을 조심해야 한다.

프로그램이 실행될 때 프로그램은

메모리에 정보를 저장하고 이용하는데 이 때 메모리의 구조는

크게 코드 영역, 데이터 영역, 힙 영역, 스택 영역으로 나뉜다.

재귀를 이용할 때 스택영역이 중요하다.

Activation Record

함수가 실행될 때 스택 영역에 activation record가 쌓인다.

activation record는 특정 함수를 실행하기 위해서 기록해두어야 하는 데이터를 의미한다.

함수 내에서 또 다른 함수를 실행하는 경우가 많다.

이러한 경우 A 함수를 실행하는 중에 B 함수가 실행 되면 다음과 같은 과정이 진행된다.

A 함수를 실행했던 데이터를 메모리의 call stack에  activation record를 기록해둔다.

B 함수의 실행이 끝나면 A 함수가 실행되던 정보를 불러오기 위해 call stack에 저장된 activation record를 불러와서

다시 A 함수를 실행할 수 있다.

즉 특정 함수를 실행할 때 그 정보를 call stack의 activation record에 기록하는 것이다.

그런데 프로그램이 사용하는 메모리는 무한한 자원이 아니다.

즉 스택 영역도 한정된 자원이다.

이 말은 함수를 재귀적으로 무한히 호출하다보면 activation record가 무한히 생성되고

이는 프로그램이 사용할 수 있는 call stack의 범위를 넘어서게 된다.

이러면 Stack Overflow 현상이 발생하는 것이다!

다만 헷갈리지 말아야할 점은 함수가 재귀적으로 무한히 실행되는 것은

activation record가 계속 쌓여서 문제가 발생하지만,

재귀적으로 실행되지 않고 일반적인 함수가 계속해서 실행되는 것은 Stack Overflow가 발생하지 않는다.

왜냐하면 함수의 실행이 끝나면 call stack에 저장된 activation record도 메모리에서 지워져서

계속 쌓이지 않기 때문이다.

그래서 base condition, 기저사례를 잘 설정해서

재귀함수를 실행하면 함수가 stack Overflow가 발생하지 않도록

잘 설계하는 것이 중요하다.

stack Overflow 발생 가능

int sum(int n){
	if (n==1) return 1
    return sum(n-1) + n;
}

위 경우 n이 엄청 커진다면 activation record가 계속 기록하여 stack overflow가 발생할 수 있다.

stack Overflow 발생 안함

while(1){
	int sum(int n, int m){
		return n + m;
	}
}

하지만 이 경우에는 함수를 실행하고 activation record를 기록하고 함수가 끝나면 바로 지우고

기록하고 지우고를 반복하여 함수는 무한히 실행하지만 실제 stack에 activation record가 무한히 쌓이는 상황은 아니다.

activation record는 몇개까지 쌓을 수 있을까?

간단한 더하기 함수를 재귀적으로 구현했을 때

함수를 4000번 정도 실행하면 Stack Overflow가 발생하는 것을 확인할 수 있었다.

이 말은 만약 재귀적으로 구현할 때 함수를 4000번 이상 실행해야 한다면 

해당 문제를 재귀적으로 해결할 수 없다는 것을 의미한다.

이때는 반복문을 이용해서 해결해야 할 것이다.

Heap Overflow?

본문과는 크게 관련없지만, 

메모리 구조에서 코드와 데이터 영역은 프로그램을 실행할 때 한번 메모리에 할당되고 크기가 변하지 않기 때문에 정적이다.

하지만 힙 영역과 스택 영역은 프로그램이 동작하는 과정에서 동적으로 이용된다.

이때 메모리가 동적으로 이용된다는 말은 프로그램이 진행하면서 계속 메모리를 일정하게 이용하는 것이 아닌,

프로그램의 진행 상황에 따라 메모리의 사용량이 변화하는 것을 의미한다.

스택을 보면 함수를 실행할 때마다 Activation Record를 기록하기 위해 메모리를 추가적으로 사용한다.

힙 영역은 프로그램 코드에서 메모리를 동적으로 할당할 때 사용된다.

주로 C, C++계열 언어에서 포인터와 new 키워드를 활용하여 힙 메모리를 할당받아 사용하는 것이 예시이다.

그렇다면 Heap Overflow도 존재하지 않을까 하는 의문이 들었다.

이에 대해 찾아보니 프로그래머가 메모리를 계속 동적으로 하고 반환해주지 않는다면

stack과 마찬가지로 heap도 overflow가 발생한다고 한다.

https://www.acmicpc.net/problem/1167

1.문제설명

트리의 지름을 구하는 방법은 다음과 같다.

아무 노드 A를 택하고, A노드와 가장 멀리있는 노드 B를 찾는다.(BFS or DFS 아무거나 사용해도 된다)

그리고 노드 B와 가장 멀리 있는 노드 C를 찾아서

노드 B와 노드 C의 거리를 구하면 그게 트리의 지름이 된다.

현재 문제에서 노드간의 거리가 다른데

이 문제는 최단경로를 찾는 문제가 아니므로 다익스트라 알고리즘을 사용할 필요는 없고

BFS로 가장 먼 거리에 있는 노드를 찾아주기만 하면된다.

2.문제풀이코드

import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

class Pair{
    int node , dist;
    Pair(int node, int dist){
        this.node = node;
        this.dist = dist;
    }
}

public class main {
    static ArrayList<Pair>[] adj;
    static int V;
    static Queue<Pair> Q;

    //start node로 부터 가장 멀리 있는 node와 거리를 구하는 함수
    static Pair bfs(int start){
        int end = 0;
        int dist = 0;
        boolean[] visit = new boolean[V+1];
        visit[start] = true;
        Q.add(new Pair(start, 0));

        while(!Q.isEmpty()){
            Pair cur = Q.poll();
            if(cur.dist > dist){
                end = cur.node;
                dist = cur.dist;
            }

            for(int i=0; i<adj[cur.node].size(); i++){
                int nextNode = adj[cur.node].get(i).node;
                int addDist = adj[cur.node].get(i).dist;

                if(!visit[nextNode]){
                    visit[nextNode] = true;
                    Q.add(new Pair(nextNode, cur.dist + addDist));
                }
            }
        }

        return new Pair(end, dist);
    }



    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        V = Integer.parseInt(st.nextToken());
        adj = new ArrayList[V+1];
        Q = new LinkedList<>();

        for(int i=1; i<=V; i++){
            adj[i] = new ArrayList<>();
        }

        for(int i=1; i<=V; i++){
            st = new StringTokenizer(br.readLine());
            int curNode = Integer.parseInt(st.nextToken());
            int connectNode = Integer.parseInt(st.nextToken());
            
            while(connectNode!=-1){
                int dist = Integer.parseInt(st.nextToken());
                adj[curNode].add(new Pair(connectNode, dist));
                connectNode = Integer.parseInt(st.nextToken());
            }
        }

        Pair start = bfs(1);
        Pair ans = bfs(start.node);
        bw.write(ans.dist+"");
        bw.flush();
        bw.close();
    }
}